Ejemplo de ecuaciones lineales:

• Ejemplo 1

Solución por sustitución

Despejamos en la primera ecuación la $x$:

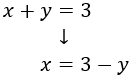
Y la sustituimos en la segunda:

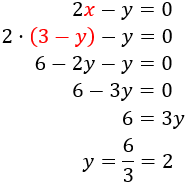
Calculamos $x$ sabiendo $y=2$:

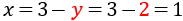
Por tanto, la solución del sistema es

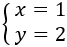
Igualación

Despejamos en ambas ecuaciones la $\mathrm{y:}$

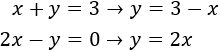
Como $y=y$, igualamos las expresiones y resolvemos la ecuación:

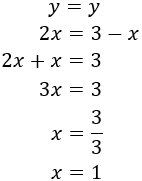
Ahora, sustituimos el valor de la incógnita $x=1$ en la primera de las ecuaciones anteriores para calcular $y$:

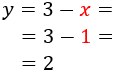
Por tanto, la solución del sistema es

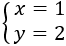
Reducción

Para sumar las ecuaciones y que desaparezca una de las dos incógnitas, los coeficientes de dicha incógnita deben ser iguales pero de signo distinto. Para ello, multiplicamos por -2 la primera ecuación.

Después, sumamos las ecuaciones y resolvemos la ecuación obtenida:

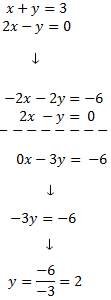
Finalmente, sustituimos el valor de $y=2$ en la primera ecuación y la resolvemos:

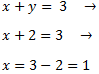
Ejemplo N°2

¿Cómo resolver problemas con ecuaciones lineales?

Referencias bibliográficas

• https://www.matesfacil.com/ESO/Ecuaciones/resueltos-sistemas-ecuaciones.html

• https://www.portaleducativo.net/segundo-medio/45/sistema-de-ecuaciones-lineales